| ■Pre | ■Up | ■Next |
x∈πとする.
a) xに強い意味で優越するx∈πが存在しないとき,xを弱パレート最適解という.
b) xに優越するx∈πが存在しないとき,xをパレート最適解という.
目的関数が二つの場合のパレート最適解の例を以下に示す.
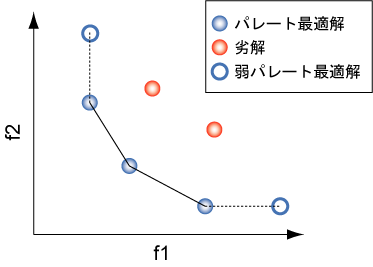
図:パレート最適解の概念
一般に,パレート最適解集合が形成する面のことをパレート最適解集合が形成する面のことをパレート最適フロントと呼ぶ.上図で示すように,一般にパレート最適解は複数存在する.
|
|||
| ■2.2 パレート最適解 | |||
| x∈πとする. a) xに強い意味で優越するx∈πが存在しないとき,xを弱パレート最適解という. b) xに優越するx∈πが存在しないとき,xをパレート最適解という. 目的関数が二つの場合のパレート最適解の例を以下に示す.
図:パレート最適解の概念 一般に,パレート最適解集合が形成する面のことをパレート最適解集合が形成する面のことをパレート最適フロントと呼ぶ.上図で示すように,一般にパレート最適解は複数存在する. |