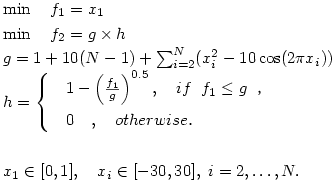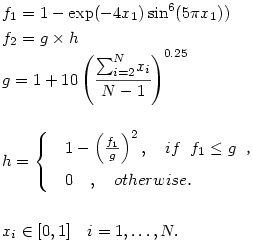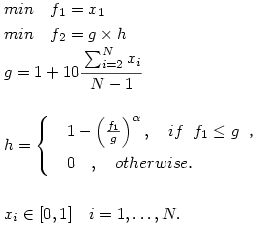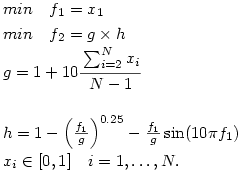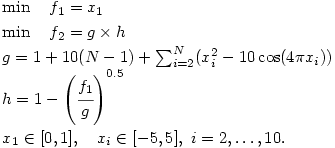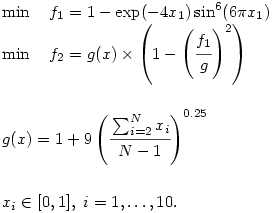| ■Pre | ■Up | ■Next |
多目的GAの性能調査,あるいは比較するために用いられるテスト問題について紹介する.
考案者[論文]
Deb [2] 多峰性のある問題 Deb [2] 偏重パレートフロント Deb [2] パラメータによって凹,凸パレートフロントを選択可能 Deb [2] 不連続なパレートフロント Zitzler,Deb [3] 10設計変数の多峰性を有する問題 Zitzler,Deb [3] 10設計変数の問題.f1(x)とx1の間に偏りがある Frank Kursawe [4] 設計変数の数は任意
Debの考案した多峰性を有する多目的最適化問題である.論文において,設計変数の数は10およびそれ以上を推奨している.
Texソース
\begin{eqnarray*}
\begin{array}{l}
\min \quad f_{1}=x_{1}\\
\min \quad f_{2}=g\times{h}\\
g=1+10(N-1)+{\sum^{N}_{i=2}}{(x_{i}^{2}-10\cos(2\pi{x_{i}}))}\\
h = \begin{cases}
& 1-\left( {\frac{f_1}{g}} \right)^{0.5},\quad if f_1\leq g \hspace{2mm} ,\\
& 0 \quad ,\quad otherwise.\\
\end{cases} \\\\
x_1\in [0,1], \quad
x_i\in [-30,30],\ i= 2,\dots ,N.
\end{array}
\label{Deb_multiModal}
\end{eqnarray*}
■ Biased Pareto-optimal front(偏重パレートフロント)
Debの考案したパレートフロントが偏重な多目的最適化問題である.論文において,設計変数の数は10およびそれ以上を推奨している.
Texソース
\begin{eqnarray*}
\begin{array}{l}
\min \quad f_{1}=x_{1}\\
\min \quad f_{2}=g\times{h}\\
g=1+10(N-1)+{\sum^{N}_{i=2}}{(x_{i}^{2}-10\cos(2\pi{x_{i}}))}\\
h = \begin{cases}
& 1-\left( {\frac{f_1}{g}} \right)^{0.5},\quad if f_1\leq g \hspace{2mm} ,\\
& 0 \quad ,\quad otherwise.\\
\end{cases} \\\\
x_1\in [0,1], \quad
x_i\in [-30,30],\ i= 2,\dots ,N.
\end{array}
\label{Deb_multiModal}
\end{eqnarray*}
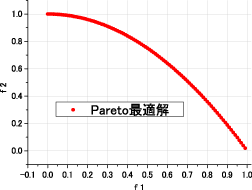
■ Concave Pareto-optimal front(くぼみのあるパレートフロント)
Debの考案したくぼみのあるパレートフロント持つ多目的最適化問題である.この問題はα=0..5のとき凸型パレート最適フロント,
α=2.0のとき非凸型パレート最適フロントとなる.また,設計変数の数は10およびそれ以上を推奨している.
Texソース
\begin{eqnarray*}
\begin{array}{l}
min \quad f_1 = x_1\\
min \quad f_2 = g \times h\\
g = 1+10 \cfrac{\sum_{i=2}^N x_i}{N-1}\\\\
h = \begin{cases}
& 1-\left( {\frac{f_1}{g}} \right)^\alpha,\quad if \hspace{2mm} f_1\leq g \hspace{2mm} ,\\
& 0 \quad ,\quad otherwise.\\
\end{cases} \\\\
x_i\in [0,1] \quad i= 1,\dots ,N. \\
\end{array}
\label{Deb_concave}
\end{eqnarray*}
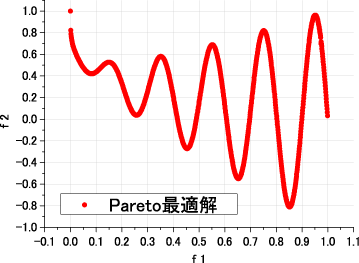
Discontinuous Pareto-optimal front(不連続なパレートフロント)
Debの考案した不連続なパレートフロント持つ多目的最適化問題である.設計変数の数は10およびそれ以上を推奨している.
Texソース
\begin{eqnarray*}
\begin{array}{l}
min \quad f_1 = x_1\\
min \quad f_2 = g \times h\\
g = 1+10 \cfrac{\sum_{i=2}^N x_i}{N-1}\\\\
h = 1-\left( {\frac{f_1}{g}} \right)^{0.25}-\frac{f_1}{g}\sin(10\pi f_1)\\
x_i\in [0,1] \quad i= 1,\dots ,N. \\
\end{array}
\label{Deb_discontinuous}
\end{eqnarray*}
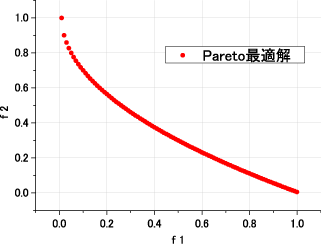
■ ZDT4
ZDT4は,10設計変数からなる2目的の多峰性を有する問題である.この問題は,xi 以外の設計変数値のとる範囲が広いため,
パレート最適解xi = 0.0を見つけ出すことが難しいという特徴をもっている.
Texソース
\begin{equation*}
\begin{array}{l}
\min \quad f_{1}=x_{1}\\
\min \quad f_{2}=g\times{h}\\
g=1+10(N-1)+{\sum^{N}_{i=2}}{(x_{i}^{2}-10\cos(4\pi{x_{i}}))}\\
h=1-\left(\cfrac{f_{1}}{g}\right)^{0.5} \\
x_1\in [0,1], \quad
x_i\in [-5,5],\ i= 2,\dots ,10.
\end{array}
\end{equation*}
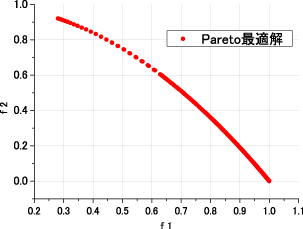
■ ZDT6
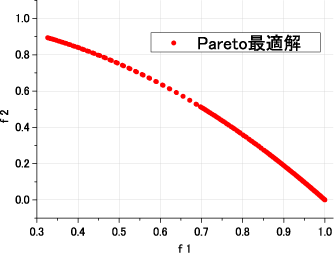
ZDT6は f1(x)とx1の間に偏りが存在するという特徴がある.
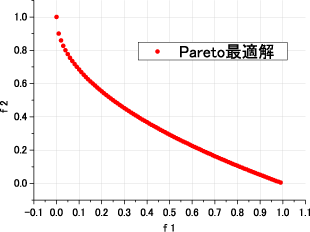
Pareto最適解
Texソース
\begin{eqnarray*}
\begin{array}{l}
\min \quad f_1=1-\exp (-4x_1)\sin ^6(6\pi x_1)\\
\min \quad f_2=g(x)\times \left( 1- \left( \cfrac{f_1}{g} \right)^{2}\right) \\\\
g(x)= 1+9 \left( \cfrac{\sum_{i=2}^{N}x_i}{N-1} \right) ^{0.25} \\\\
x_i\in [0,1],\ i= 1,\dots ,10. \\
\end{array}
\label{ZDT6}
\end{eqnarray*}
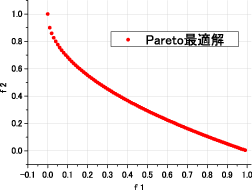
■ KUR
KURはf1(x)において連続する2変数間の相互作用を持ち,f2(x)において多峰性を有する問題である.
また,KURのパレート最適解は未知である.
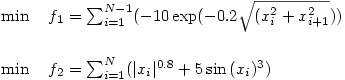
Texソース
\begin{eqnarray*}
\begin{array}{l}
\min \quad f_1=\sum^{N-1}_{i=1}(-10\exp(-0.2\sqrt{(x^2_i+x^2_{i+1}}))\\\\
\min \quad f_2=\sum^{N}_{i=1}(|x_i|^{0.8}+5\sin{(x_i)^3})
\label{KUR}
\end{array}
\end{eqnarray*}