| ■Pre | ■Up | ■Next |
1.はじめに
多目的最適化問題においてパレート最適解を求める場合,得られた解が目的関数もしくは設計変数空間上の広範囲かつ真のパレート解付近に求まっていることが重要な要素である.広範囲に広がる解を求めるためには,次の二点が必要な要素となる.まず解が集中するのではなく均等に存在すること,二つ目に各目的関数を単一目的とした際の最適解が得られていることである.
2.DCMOGA ( Distributed Cooperation model of MOGA and SOGA )
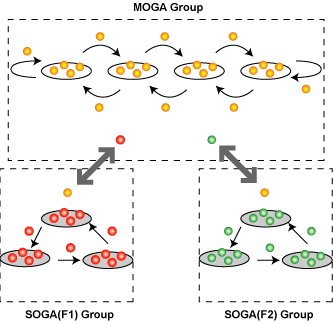
多目的分散協力型モデル(DCMOGA)では,解の広がりを持ったパレート最適解の探索を目的とし,各目的関数の最適解とパレートフロントの前進を同時に行う手法を提案している. DCMOGAでは,多目的GAを行う個体群(MOGA個体群)と,各目的関数における最適解を探索する個体群(SOGA個体群)を用いて探索を行い,ある一定期間毎に最適解を交換することで協調して解探索を行う.この手法により,より広範囲に分布し,かつ精度の高いパレート最適解の探索を図る.以下に2目的の場合の DCMOGAのイメージを図示する.

3.DCMOGAの流れ
最小化問題におけるn目的の多目的最適化問題の場合,DCMOGAは次のように探索を進める.
STEP1.
総個体数分の個体をランダムに発生させる.
STEP2.
MOGA個体群と各目的関数Fi(i=1,2,...n)の最適解を探索する n個のSOGA個体群に分割する.
SOGA個体群は1以上の島で構成される.
STEP3.
与えられた評価計算回数まで,各個体群が独立して探索を行う.
STEP4.
MOGA個体群が各SOGA個体群と個体情報を交換する.(移住)
・目的関数Fiの探索を行うSOGA個体群が,個体群内の最適解 I SをMOGA個体群に送信する.
・MOGA個体群は,群内でFiの最良値を持つ最適解I M を送信する.
STEP5.
目的関数Fiにおいて,各個体群の最適解であるIS とIMを比較し,次回の移住までの各個体群の評価計算回数を決定する.
・IS < IMの場合:SOGA個体群の評価計算回数を減少させ,MOGA個体群の評価計算回数を増加させる.
・IM ≤ ISの場合:上記と逆の操作を行う.
STEP6.
現段階までの各個体群の評価計算回数を合計し,終了評価計算回数と比較する.
終了評価計算回数に満たなければ,STEP3に戻る.