MOGAでは，非劣解集合の多様性を保持するために，各ランク間においてニッチングを行っている．このニッチングは以下のようなシェアリング関数を用いている．

di,jは目的関数空間での個体iとjのユークリッド距離である．下記の式で求められる．

シェアリング関数によって個体間の混雑度を示すニッチカウントを求め，そのニッチカウントを各個体の適合度に作用させることによって個体の多様性を保持することができる． ニッチカウントは下記の式で求めることができる．

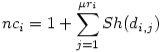
ここで，ニッチカウントの初期値は1で，μriはランクriにおける個体の数を示している．

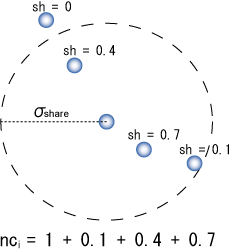
図：ニッチカウント